알고리즘 공부순서
https://gooddaytocode.blogspot.com/2016/05/blog-post_6.html
알고리즘과 입/출력
시간복잡도
시간복잡도는 문제해결에 걸리는 시간, 입력의 함수 관계를 가리킨다. 컴퓨터 과학에서 알고리즘이 시간 복잡도는 입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화하는 것이다. 알고리즘의 시간복잡도는 주로 빅 오 표기법을 써서 나타내며 이 빅오 표기법은 계수와 낮은 차수의 항을 제외시키는 방법이다.
빅오 표기법
- 출처: https://coding-factory.tistory.com/608
'아무리 많이 걸려도 이 시간 안에는 끝날 것' 의 개념이 중요하다. 예를 들어 동전을 튕겨서 뒷면이 나올 확률을 이야기해본다면 운이 좋으면 한 번에 뒷면이 나올 수도 있고 운이 좋지 않으면 3번 4번만에 뒷면에 나올 수도 있다. 운이나쁜 경우 n번만큼 동전을 튕겨야 하는 최악의 경우가 발생하는데 이 최악의 경우를 계산하는 방식을 빅오(Big-O) 표기법이라고 부른다.
O(1) Constant
- 입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘
- 데이터가 얼마나 증가하던 성능에 영향이 없다.
O(log₂ n) Logarithmic
- 입력 데이터의 크기가 커질수록 처리 시간 로그(log: 지수 함수의 역함수)만큼 짧아지는 알고리즘
- 데이터가 10배가 되면, 처리시간은 2배가 된다. 이진 탐색이 대표적이며, 재귀가 순기능으로 이루어 지는 경우도 해당한다.
O(n) Linear
- 입력 데이터의 크기에 비례해 처리 시간이 증가하는 알고리즘
- 데이터가 10배가 되면, 처리 시간도 10배가 된다 , 1차원 for문
O(n log₂ n) (Linear-Logarithmic)
- 데이터가 많아질수록 처리시간이 로그(log) 배 만큼 더 늘어나는 알고리즘
- 데이터가 10배가 되면, 처리 시간는 20배가 된다
- 정렬 알고리즘 중 병합정렬, 퀵정렬
O(n2) (quadratic)
- 데이터가 많아질수록 처리시간이 급수적으로 늘어나는 알고리즘
- 데이터가 10배가 되면, 처리 시간은 최대 100배가 된다. 이중 루프 (n² matrix)가 대표적이며 단, m이 n보다 작을 때는 반드시 O(nm)로 표시하는 것이 바람직하다.
O(2ⁿ) (Exponential)
- 데이터량이 많아질수록 처리시간이 기하급수적으로 늘어나는 알고리즘
- 대표적으로 피보나치 수열이 있으며, 재귀가 역기능을 할 경우도 해당됨.
자료구조
- 출처: https://helloworldjavascript.net/pages/282-data-structures.html
스택 (Stack)
- 한쪽 끝에서만 데이터를 넣고 뺼 수 있는 제한적으로 접근 가능한 후입선출(Last-In First-Out) 형태의 선형 자료구조
- 기본적으로 후입선출(나중에 들어온 데이터가 가장 먼저 나가는) 구조로 이루어져 있음
pop(): 스택에서 가장위에 있는 항목을 제거한다
push(item): item 하나를 스택의 가장 윗 부분에 추가한다
peek: 스택의 가장 위에 있는 항목을 반환한다
isEmpty(): 스택이 비어 있을 때 true를 반환한다.
class Stack {
constructor() {
this.array = [];
this.index = 0;
}
print() {
console.log('print: ', this.array);
}
push(item) {
this.array[this.index++] = item;
}
pop() {
this.index--;
let popVal = this.array[this.index];
this.array.length = this.index;
return popVal;
}
peek() {
return this.array[this.index - 1];
}
isEmpty() {
return this.array.length === 0;
}
}
let stack = new Stack();
stack.push(1); //[1]
stack.push(2); //[1, 2]
stack.push(3); //[1, 2, 3]
stack.push(4); //[1, 2, 3, 4]
stack.push(5); //[1, 2, 3, 4, 5]
stack.print(); //[1, 2, 3, 4, 5]
stack.pop(); //[1, 2, 3, 4]
console.log('peek: ', stack.peek()); //4
stack.pop(); //[1, 2, 3]
stack.pop(); //[1, 2]
stack.pop(); //[1]
stack.pop(); //[]
console.log('isEmpty: ', stack.isEmpty()); stack.pop(); //true
큐 (Queue)
- 데이터를 집어넣을 수 있는 선형(linear) 자료형
- 먼저 집어넣은 데이터가 먼저 나온다. FIFO(First In First Out) 선입선출
- 데이터를 집어넣는 enqueue, 데이터를 추출하는 dequeue 등의 작업이 가능하다
class Queue {
constructor() {
this.array = [];
this.front = 0; //첫 요소의 포인트
this.rear = 0; //마지막 요소의 포인트
}
print() {
console.log('print: ', this.array);
}
isEmpty() {
return this.array.length === 0;
}
enqueue(item) {
this.array[this.rear++] = item;
}
dequeue() {
if(this.isEmpty()) {
return false;
}
let dequeuedValue = this.array[this.front];
this.front++;
return dequeuedValue;
}
}
let queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
queue.print(); // print: (3) [1, 2, 3]
console.log(queue.dequeue()); // 1
console.log(queue.dequeue()); // 2
console.log(queue.dequeue()); // 3
덱 (Deque)
Deque는 "Double-ended Queue"의 줄임말로, 양쪽 끝에서 삽입과 삭제가 모두 가능한 자료 구조입니다. 일반적으로는 앞(front)과 뒤(rear)에서 모두 삽입과 삭제가 가능하도록 설계되어 있습니다. Deque는 큐(Queue)와 스택(Stack)의 특성을 모두 가지고 있어 다양한 상황에서 유용하게 사용될 수 있습니다.
class Deque {
constructor() {
this.array = [];
}
print() {
console.log(this.array);
}
isEmpty() {
return this.array.length === 0;
}
//front 요소 추가
addFront(item) {
this.array.unshift(item);
}
//rear 요소를 추가
addRear(item) {
this.array.push(item);
}
//front 요소 삭제 후 반환
removeFront() {
if(this.isEmpty()) {
return false;
}
return this.array.shift();
}
//rear 요소 삭제 후 반환
removeRear() {
if(this.isEmpty()) {
return false;
}
return this.array.pop();
}
}
let deque = new Deque();
deque.addFront(1);
deque.addFront(2);
deque.addFront(3);
deque.print(); //[3, 2, 1]
deque.addRear(6);
deque.addRear(5);
deque.addRear(4);
deque.print(); //[3, 2, 1, 6, 5, 4]
deque.removeFront(); // [2, 3, 6, 5, 4]
deque.print();
deque.removeRear(); // [2, 3, 6, 5]
deque.print();
다이나믹 프로그래밍
특정 범위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘,
(접근방식은 분할 정복 알고리즘과 비슷하다)
피보나치 수열 Fibonacci numbers
출처: https://m.blog.naver.com/prayer2k/222432519342
토끼 한 쌍이 있다. 한 쌍의 토끼는 한 달이 지나면 성장을 하고, 그 다음 한달 후 부터 매달 암 수 한 쌍의 새끼를 낳는다(두 달 후 부터 매달 한 쌍의 토끼를 낳는 것이다) 태어난 토끼 한 쌍도 마찬가지다. 한 달 동안 성장하고, 그 다음 한 달이 지나면서 매달 한 쌍의 토기를 낳는다. 1년이 지나면 몇 쌍의 토끼가 있을까?
*조건
- 첫 달에는 새로 태어난 토끼 한 쌍만이 존재한다
- 두 달 이상이 된 토끼는 번식 가능하다
- 번식 가능한 토끼 한 쌍은 매달 새끼 한 쌍을 낳는다.
- 토끼는 죽지 않는다.
처음: A 1쌍
1개월: A - 1쌍
2개월: A B(new) - 2쌍
3개월: A C(new) B - 3쌍
4개월: A B D(new) E(new) C - 5쌍
5개월: A B C F(new) g(new) h(new) D, E - 8쌍
1, 1, 2, 3, 5, 8
f(n) = f(n-1) + f(n-2)
n 번째 달의 토끼 쌍은,
n - 1번째 달의 토끼 쌍 개수에
n - 2번째 달의 토끼 쌍의 개수를 더한다.
/*
f(n) = f(n - 1) + f(n - 2);
*/
function fibonacci(n) {
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
console.log(fibonacci(5)); // 8
3가지 대표적인 문제
1. 막대기 자르기 문제
2. 최장 공통 부분 수열 문제
3. 0/1 배낭 문제
- (23/11/14) 문제 하나도 모르겠네 ㅎㅎ;
수학
나머지 연산
(Modulo 연산)은 양의 정수들 사이에서 두 수를 나누고 남은 나머지를 구하는 연산. 보통 % 기호로 표시됨
예를 들어, 7을 3으로 나누면 몫은 2이고 나머지는 1이다. 따라서 7을 3으로 나눈 나머지는 1이 된다.
7 % 3 = 1
//홀수 짝수 판별
function modulo1(n) {
if(n % 2 === 0) {
return '짝수';
} else {
return '홀수';
}
}
console.log(modulo1(2)); //짝수
console.log(modulo1(3)); //홀수
console.log(modulo1(112)); //짝수
console.log(modulo1(389)); //홀수
서로소
- 두 수 사이의 관계에서 공통되는 약수가 최대 1이며 1밖에 없는 수를 뜻한다.
5의 약수: 1, 5
6의 약수: 1, 2, 3, 6
: 5, 6의 약수 중 두 수의 일치하는 공약수가 1이 존재하므로 서로소의 기준에 적합하여
서로서라고 할 수 있다.
12의 약수: 1 2 3 4 6 12
27의 약수: 1 3 9 27
: 1, 3의 공약수가 존재하기 때문에 서로소가 아니다.
최대 공약수와 최소 공배수
두 수를 소인수분해를 한 뒤, 두 수의 공통된 소인수를 모두 곱하면 최대 공약수, 두수의 모든 소인수를 곱하면 최소공배수가 된다.
120, 36
120 = 2 x 2 x 2 x 3 x 5
36 = 2 x 2 x 3 x 3
공통된 소인수: 2 x 2 x 3
두 수의 모든 소인수 : 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 5
최대공약수(=공통된 소인수 곱하기) = 12
최소공배수(두 수의 모든 소인수 곱하기) 360
최대 공약수 (GCD, Greatest Common Divisor) 와 최소 공배수(LCM, Least Common Multiple)를 구하는 알고리즘에는 여러가지 방법이 있습니다.
1. 유클리드 호제법을 이용한 최대 공약수(GCD) 구하기
: 유클리드 호제법은 두 수의 최대 공약수를 구하는 방법 중 가장 일반적이고 효율적인 방법이다. 두 수 A와 B에 대해 A를 나눈 나머지를 구하고, 그 나머지를 B로 대체하는 과정을 반복하여 나머지가 0이 되는 순간 B가 최대 공약 수 가 된다.
호제법: 두 수가 서로 상대방 수를 나누어 결국 원하는 수를 얻는 알고리즘
120, 36
1. 120은 36로 나누어 떨어지지 않기 때문에 120을 36로 나눈 나머지를 구한다
3
_____
36 | 120
108
____
12 -> 나머지
2. 36은 12로 나누어 떨어지지 않기 때문에 36을 12로 나눈 나머지를 구한다
3
______
12 | 36
36
0
-> 36은 12로 나누어 떨어진다.
-> 최대공약수는 12
//유클리드 호제법을 이용한 최대 공약수(GCD) 구하기
function euclid(a, b) {
if(b === 0) {
return a;
} else {
return euclid(b, a % b);
}
}
console.log(euclid(120, 36)); // 12
최소 공배수 (LCM) 구하기
최소 공배수는 두 수의 곱을 최대 공약수로 나누어 구할 수 있다.
//최소 공배수
function euclid2(a, b) {
return a * b / euclid(a, b);
}
console.log(euclid2(120, 36)); // 360
소수
소수(Prime number)는 1과 자기 자신 이외에는 어떤 수로도 나누어 떨어지지 않는 수를 의미한다. 소수를 판별하는 알고리즘은 여러가지 방법으로 구현 할 수 있다.
* 에라토스테네스의 체(Sieve of Eratoshenes) 알고리즘
: 이 알고리즘은 주어진 범위 내의 모든 소수를 찾는 데 사용된다.
1. 2부터 시작해서 N까지의 모든 수를 배열에 넣는다.
2. 2는 소수이므로 2의 배수들을 소수 목록에서 제외한다
3. 다음으로 남아있는 수(3부터 시작하는 다음 소수)의 배수들을 소수 목록에서 제거한다
4. 위 과정을 반복하여 끝까지 진행한다. 남아 있는 수들이 소수 이다.
function primeNumber(n) {
let prime = new Array(n + 1).fill(true);
//0과 1은 소수가 아니다
prime[0] = prime[1] = false;
for(let i=2; i<=n; i++) {
if(prime[i]) {
for (let j = i * i; j <= n; j += i) {
prime[j] = false;
}
}
}
for(let i=2; i<=n; i++) {
if(prime[i]) {
console.log(i); // 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
}
}
}
primeNumber(30);
소인수 분해 (Factorization)
주어진 수를 소수들의 곱으로 표현하는 것을 말한다. 이 과정에서 주어진 수를 나눌 수 있는 작은 소수로 계속해서 나누어 가는 방법을 사용한다
1. 2부터 시작해서 주어진 수가 2로 나누어질 때 까지 나눈다
2. 이후에는 홀수 소수(3, 5, 7) 들을 나누며 소수들을 계쏙해서 나누어 가는 과정을 반복한다
3. 마지막으로 남은 값이 2보다 큰 경우는 소수이므로 해당 값을 출력한다
// [36]
// - 36 / 2 = 18
// - 18 / 2 = 9
// - 9 / 3 = 3
// : 2 x 2 x 3 x 3
function factorization(n) {
while(n % 2 === 0) {
console.log(2);
n = n / 2;
}
for(let i=3; i<=n; i = i + 2) {
while(n % i === 0) {
console.log(i);
n = n / i;
}
}
if(n > 2) {
console.log(n);
}
}
factorization(36);
// 36 = 2 x 2 x 3 x 3
진법 변환
숫자를 다른 진법으로 표현하는 것.
ex) 10진법의 숫자 13을 2진법으로 변환하는 경우
13 / 2 = 6 ... 1
6 / 2 = 3 ... 0
3 / 2 = 1 ... 1
1 / 2 = 0 ... 1
-> 1101
//10진법 -> 2진법
function binary(n) {
let binaryNumber = '';
while(n > 0) {
binaryNumber = (n % 2) + binaryNumber;
n = Math.floor(n / 2);
}
return binaryNumber;
}
console.log(binary(13)); //1101
ex) 2진법에서 10진법으로 변경
(1 * 2^3) + (1 * 2^2) + (0 * 2^1) + (1 * 2^0)
= ( 1 * 8 ) + ( 1 * 4 ) + ( 0 * 2 ) + ( 1 * 1)
= 8 + 4 + 0 + 1
= 13
//2진법 -> 10진법
function binaryToDecimal(n) {
let decimal = 0;
let power = 0;
for(let i= n.length - 1; i >= 0; i--) {
decimal += parseInt(n[i] * Math.pow(2, power));
power++;
}
return decimal;
}
console.log(binaryToDecimal('1101')); //13
팩토리얼
양의 정수 n에 대해 1부터 n까지의 모든 정수를 곱한 값을 의미한다. 일반적으로 n!로 표현하며, 수학적으로 아래와 같이 표현된다.
n! = n (n - 1) x (n - 2) x .... x 2 x 1
즉, 팩토리얼은 해당 수부터 1까지의 모든 양의 정수를 곱한 값을 의미한다.
5!
= 5 x 4 x 3 x 2 x 1
= 120
function factorial(a) {
if(a === 0 || a === 1) {
return 1;
} else {
return a * factorial(a - 1);
}
}
console.log('5! : ', factorial(5)); //120
정렬
STL의 sort를 응용하는 방법
O(NlgN) 정렬 알고리즘
퀵 소트와머지 소트는 분할 정복 챕터
힙 소트는 자료구조 2챕터
(?)
삽입 정렬
출처 : https://www.zerocho.com/category/Algorithm/post/57e39fca76a7850015e6944a
: 여러 개의 섞인 숫자가 있을 때, 그 숫자를 작은 순서부터 큰 순서로 정렬하는 것. 삽입 정렬은 첫 숫자는 놔두고, 두 번쨰 자리 숫자부터 뽑아서 그 숫자가 첫 숫자보다 크면 첫 숫자 오른쪽에, 작으면 왼쪽에 넣습니다. 세 번째 숫자를 뽑아서 앞의 두 숫자와 크기를 비교해서 알맞은 자리에 넣습니다.
ex) [5, 6, 1, 2, 4, 3]
[5, 6, 1, 2, 4, 3]
: 두 번째 숫자, 6은 5보다 크니까 그대로
[5, 6, 1, 2, 4, 3]
: 1은 5, 6 보다 작으니까 맨 앞으로
-> [5, 1, 6, 2, 4, 3]
-> [1, 5, 6, 2, 4, 3]
[1, 5, 6, 2, 4, 3]
: 2는 5, 6 보다 작고, 1보다 크니까 이동
-> [1, 5, 2, 6, 4, 3]
-> [1, 2, 5, 6, 4, 3]
[1, 2, 5, 6, 4, 3]
: 4는 5, 6, 보다 작고 , 2보다 크니까 이동
-> [1, 2, 5, 4, 6, 3]
-> [1, 2, 4, 5, 6, 3]
[1, 2, 4, 5, 6, 3]
: 3도 위와 동일
=> [1, 2, 3, 4, 5, 6]
var insertionSort = function(array) {
var i = 1, j, temp;
for (i; i < array.length; i++) {
temp = array[i]; // 새로운 숫자를 선택함
for (j = i - 1; j >= 0 && temp < array[j]; j--) { // 선택한 숫자를 이미 정렬된 숫자들과 비교하며 넣을 위치를 찾는 과정, 선택한 숫자가 정렬된 숫자보다 작으면
array[j + 1] = array[j]; // 한 칸씩 뒤로 밀어낸다
}
array[j + 1] = temp; // 마지막 빈 칸에 선택한 숫자를 넣어준다.
}
return array;
};
insertionSort([5, 6, 1, 2, 4, 3]); // [1, 2, 3, 4, 5, 6]
합병 정렬(머지 정렬, 병합 정렬)
- 참고: https://www.zerocho.com/category/Algorithm/post/57ee1fc107c0b40015045cb4
합병정렬은 O(NlogN)이기 떄문에 성능이 준수하다. 다만 30개 이하의 숫자를 정렬할 때는 삽입 정렬과 별 차이도 없고 정렬하는데 추가적인 메모리가 필요하다는 단점이 있습니다. 보통은 재귀 함수를 사용해서 만든다.
합병 정렬은 분할 정복 알고리즘에 속한다. 유명한 수학자 폰 노이만이 개발 했다. 분할 정복이란 어떤 문제를 그대로 해결할 수 없을 때, 작은 문제를 분할해서 푸는 것을 말한다.
합병 정렬은 배열을 두개 로 나누고 나눈 것을 다시 두개로 계속 나뉘 정렬합니다.
/*
[mergeSort]
2,4,5,7,1,3,6,8
2,4,5,7 / 1,3,6,8
2,4 / 5,7 / 1,3 / 6,8
2 / 4 / 5 / 7 / 1 / 3 / 6 / 8
[merge]
1)
- left: 2, right: 4, result: 2, 4
- left: 5, right: 7, result: 5, 7
- merge([2, 4], [5, 7])
- result: 2, 4, 5, 7
2)
- left: 1, right: 3, result: 1, 3
- left: 6, right: 8, result: 6, 9
- merge([1, 3], [6, 9]);
- result: 1, 3, 6, 9
3)
- merge([2, 4, 5, 7], [1, 3, 6, 9])
- 1 , 2, 3, 4, 5, 6, 7, 9
*/
function mergeSort(arr) {
if(arr.length < 2) return arr;
let len = arr.length;
let pivot = Math.floor(len / 2);
let left = arr.slice(0, pivot);
let right = arr.slice(pivot, len);
console.log('len :', len, ' pivot: ', pivot, ' left: ', left, ' right: ', right);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
let result = [];
while(left.length && right.length) {
if(left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length) result.push(left.shift());
while (right.length) result.push(right.shift());
console.log('result: ', result);
return result;
}
console.log(mergeSort([2,4,5,7,1,3,6,8])); // [1, 2, 3, 4, 5, 6, 7, 8]
버블 정렬 (bubble sort)
* 참고: https://www.zerocho.com/category/Algorithm/post/57f67519799d150015511c38
- 정렬하는 모습이 거품이 꺼지는 모습과 비슷하기 때문
- O(n^2) : 성능이 좋지 않다.
- 주로 알고리즘 교육용을 제외하고는 사용되지 않는다.
[5,1,7,4,6,3,2,8] 처음 두 수를 비교해서 순서대로 숫자를 서로 바꿔줍니다.
[1,5,7,4,6,3,2,8] 5와 7은 이미 정렬되어 있으니까 그대로 놔둡니다.
[1,5,7,4,6,3,2,8] 7과 4는 서로 바꿔줍니다.
[1,5,4,7,6,3,2,8]
[1,5,4,6,7,3,2,8]
[1,5,4,6,3,7,2,8]
[1,5,4,6,3,2,7,8] 끝까지 정렬을 했으면 다시 처음부터 비교합니다.
[1,5,4,6,3,2,7,8]
[1,4,5,6,3,2,7,8] 5,6은 넘어가고 6,3 순서를 바꿔줍니다.
[1,4,5,3,6,2,7,8]
[1,4,5,3,2,6,7,8] 다시 처음부터 비교합니다.
[1,4,3,5,2,6,7,8]
[1,4,3,2,5,6,7,8] 다시 처음부터
[1,3,4,2,5,6,7,8]
[1,3,2,4,5,6,7,8] 다시 처음부터
[1,2,3,4,5,6,7,8] 정렬 끝
function bubbleSort(arr) {
for(let i = 0; i<arr.length; i++) {
for(let j = i + 1; j<arr.length; j++) {
if(arr[i] > arr[j]) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
console.log(bubbleSort([5,1,7,4,6,3,2,8]));
선택 정렬 (selection sort)
* 출처: https://www.zerocho.com/category/Algorithm/post/57f728c85141fc5fe4f4ca89
- 성능이 좋지 않아도 배우는 이유는 코드가 간단하고 작은 수 (보통 30이하) 에서는 효과적이다.
- 성능이 좋다고 표현되는 정렬들은 오히려 30 이하의 작은 수에서는 성능이 안 좋은 경우도 있다
배열을 처음부터 훑어서 가장 작은 수를 제일 앞에 가져다 놓는다
다시 배열을 훑어서 두 번째로 작은 수를 두번 째 칸에 가져다 놓는다
계속 반복해서 끝까지 정렬한다
[5,1,4,7,2,6,8,3] 배열을 처음부터 훑어 가장 작은 1을 앞으로 보냅니다.
[1,5,4,7,2,6,8,3] 다시 훑어 2를 앞으로 보냅니다.
[1,2,4,7,5,6,8,3] 3을 앞으로
[1,2,3,7,5,6,8,4]
[1,2,3,4,5,6,8,7]
[1,2,3,4,5,6,8,7]
[1,2,3,4,5,6,7,8] 정렬 끝
function selectionSort(arr) {
let len = arr.length;
let minIndex;
for(let i = 0; i < len; i++) {
minIndex = i;
for(let j = i + 1; j < len; j++) {
if(arr[minIndex] > arr[j]) {
minIndex = j;
}
}
let temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
console.log(selectionSort([5,1,4,7,2,6,8,3]));
// [1, 2, 3, 4, 5, 6, 7, 8]
퀵 정렬 (quick sort)
출처 : https://www.zerocho.com/category/Algorithm/post/57f72d415141fc5fe4f4ca8b
이름처럼 빠르다, 정확히는 재수가 없지 않으면 빠르다.
재수가 없으면 매우 느리다 하지만 재수 없는 매우 느리다
하지만 재수없는 경우가 희박하기 때문에 많이 사용된다
빠르기로 유명한 합병 정렬보다 평균 두 배 빠르다.
또 다른 단점으로는 같은 숫자들을 정렬할 경우 순서가 섞일 수 있다.
예를 들어, 100이 3개가 있고 각각 1번, 2번, 3번 번호가 매겨져 있을 때 퀵 정렬 방법으로 정렬하면
1, 2, 3 번호가 매겨져 있을 때 퀵 정렬 방법으로 정렬하면 1,2, 3, 순서가 아닌 다른 순서로 정렬 될 수도 있다.
- 합병 정렬 처럼 분할 정복 기법을 사용. 그 상태로 문제를 해결하지 못할 떄 작게 쪼개어 해결한다.
1. 기준 원소 (Pivot) 선택
: 배열에서 기준이 되는 하나의 원소를 선택합니다. 일반적으로 배열의 가장 왼쪽이나, 오른쪽 또는 중간에 위치한 원소를 선택한다
2. 분할 (Division)
: 선택한 기준 원솔르 기준으로 배열을 분할한다. 기준 원소보다 작은 원소들은 왼쪽으로, 큰 원소들은 오른쪽으로 옮깁니다. 이 과정을 통해 기준 원소는 최종적으로 자신이 정렬된 위치에 들어가게 된다. 이때, 기준 원소의 왼쪽은 기준 원소보다
작은 값들이, 오른쪽은 큰 값들이 위치하게 된다.
3. 재귀적으로 반복
: 분할된 두 개의 부분 배열에 대해 위 과정을 재귀적으로 반복합니다. 각부분 배열에 대해 동일한 분할 과정을 적요하면서, 부분 배열의 크기가 1또는 0이 될 떄까지 반복합니다.
4. 결합(Combine)
: 최종적으로 정렬된 부분 배열들을 결합하여 전체 배열을 정렬한다.
/*
// 7, 2, 1, 8, 6, 3, 5, 4
기준원소: 4
4보다 작을 경우 왼쪽
4보다 클 경우 오른쪽
1) 7 / L: []. R: [7]
2) 2 / L: [2], R: [7]
3) 1 / L: [2, 1], R: [7]
4) 8 / L: [2, 1], R: [7, 8]
5) 6 / L: [2, 1], R: [7, 8, 6]
6) 3 / L: [2, 1, 3], R: [7, 8, 6]
7) 5 / L: [2, 1, 3], R: [7, 8, 6, 5]
---
return [...quickSort(left), pivot, ...quickSort(right)];
return [...quickSort([2, 1, 3]), 4, ...quickSort([7, 8, 6, 5])];
---
quickSort([2, 1, 3])
[2, 1, 3] / pivot: 3
> L: [2, 1] / 3 / R: []
[2, 1] / pivot: 1
> L: [] / 1 / R: [2]
=> 1, 2, 3
---
quickSort([7, 8, 6, 5])
[7, 8, 6, 5] / pivot: 5
> L: [] / 5 / R: [7, 8, 6]
[7, 8, 6] / pivot: 6
> L: [] / 6 / R: [7, 8]
[7, 8] / pivot: 8
> L: [7] / 8 / R: []
=> 5, 6, 7, 8
---
return [...[1, 2, 3]), 4, ...[5, 6, 7, 8]];
-> [1, 2, 3, 4, 5, 6, 7, 8]
*/
function quickSort(arr) {
if(arr.length < 2) return arr;
let pivot = arr[arr.length - 1];
let left = [];
let right = [];
for(let i = 0; i < arr.length - 1; i++) {
if(pivot > arr[i]) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return [...quickSort(left), pivot, ...quickSort(right)];
}
console.log(quickSort([7, 2, 1, 8, 6, 3, 5, 4]));
계수 정렬 (couting sort)
* 출처: https://www.zerocho.com/category/Algorithm/post/58006da88475ed00152d6c4b
O(n + k)
계수 정렬(Counting Sort)은 정렬 알고리즘 중 하나로, 입력 배열의 각 요소가 몇 번 등장하는지를 세어 정렬하는 방식입니다. 일반적으로 제한된 범위 내의 정수를 정렬할 때 효과적입니다.
function coutingSort(arr) {
let max = Math.max(...arr);
let counts = new Array(max + 1).fill(0);
for(let i = 0; i < arr.length; i++) {
counts[arr[i]]++;
}
console.log('max: ', max); //4
console.log('counts: ', counts); // [1, 1, 2, 1, 3]
let sortedIndex = 0;
for(let i = 0; i < counts.length; i++) {
while(counts[i] > 0) {
arr[sortedIndex] = i;
sortedIndex++;
counts[i]--;
}
}
return arr;
}
console.log(coutingSort([3,4,0,1,2,4,2,4])); //[0,1,2,2,3,4,4,4]
기수 정렬 (radix sort)
* 출처: https://www.zerocho.com/category/Algorithm/post/58007c338475ed00152d6c4c
- O(dn), d는 가장 큰 데이터의 자리수.
- 기수정렬은 정수나 문자열과 같은 숫자들을 자릿수를 기준으로 정렬하는 비교 없이 정렬하는 알고리즘이다. 이 알고리즘은 가장 낮은 자리수부터 시작하여 가장 높은 자리수까지 순차적으로 정렬한다.
1. 가장 낮은 자리수부터 정렬: 정렬하려는 숫자들 중에서 가장 낮은 자리수를 기준으로 정렬
2. 자릿수별로 정렬된 숫자 그룹화: 가장 낮은 자리수를 기준으로 정렬한 후 동일한 자리수를 가진 숫자들을 그룹화한다.
3. 다음 자리수로 이동: 그룹화된 숫자들을 이어붙이고, 그 다음 높은 자리수를 기준으로 정렬한다. 이 작업은 가장 높은 자리수까지 반복된다.
4. 최종 정렬된 배열: 모든 자리수에 대한 정렬이 완료되면, 최종적으로 정렬된 배열이 얻어진다.
기수 정렬의 핵심 아이디어는 숫자들을 자릿수에 따라 비교 없이 정렬하기 때문에 비교 정렬 알고리즘에 비해 성능이 우수할 수 있다. 하지만 기수 정렬은 숫자의 자릿수에 따라 반복 횟수가 결정되기 때문에 숫자가 클수록 추가적인 공간과 시간이 필요할 수 있다.
function radixSort(arr) {
let max = getMax(arr); //532, 최대값
let maxDigitCount = String(max).length; //3, 최대길이
for(let i = 0; i < maxDigitCount; i++) {
const digitBuckets = Array.from({ length: 10 }, () => []);
// 0 ~ 9 까지의 그룹을 담을 배열 생성
for(let j = 0; j < arr.length; j++) {
let mod = Math.floor(arr[j] / Math.pow(10, i)) % 10;
//현재 자리 수 숫자 추출
digitBuckets[mod].push(arr[j]);
//해당 자릿수의 숫자를 가진 그룹에 값 추가
}
arr = [].concat(...digitBuckets);
//그룹을 합쳐서 새로운 배열 생성
}
return arr;
}
//최대 값
function getMax(arr) {
let max = arr[0];
for(let i = 1; i < arr.length; i++) {
if(max < arr[i]) {
max = arr[i];
}
}
return max;
}
console.log(radixSort([532, 234, 123, 435, 323, 321, 324]));
// [123, 234, 321, 323, 324, 435, 532]
자료구조 (연결 리스트, linked list)
* 출처 : https://www.zerocho.com/category/Algorithm/post/58008a628475ed00152d6c4d
데이터 요소들을 연결된 노드(node)들의 집합으로 표현하는 선형 데이터 구조 입니다. 링크드 리스트는 각 노드가 데이터와 다음 노드를 가리키는 포인터(링크)로 구성되어있다.
기본적으로 노드는 데이터 필드와 다음 노드를 가리키는 링크 필드로 구성된다. 각 노드는 다음 노드에 대한 참조(링크)를 가지고 있어서 데이터 요소들이 메모리에서 연속적으로 저장되지 않아도 된다. 이것이 배열과의 주요한 차이점 중 하나이다.
1. 단일 연결 리스트 (Single Linked List)
- 각 노드는 데이터와 다음 노드를 가리키는 하나의 링크를 가진다
- 리스트의 첫 번쨰 노드를 가리키는 특별한 포인터인 헤드(head)가 있다.
- 각 노드는 데이터와 그 다음 노드를 가리키는 링크로 구성된다.
2. 이중 연결 리스트 (Double Linked LIst)
- 각 노드는 데이터와 이전 노드를 가리키는 링크와 다음 노드를 가리키는 링크 두개를 가진다
- 이전 노드를 가리키는 링크를 통해 리스트를 역방향으로 탐색할 수 있다
- 리스트의 시작점을 가리키는 head와 종료점을 가리키는 tail이 있을 수 있다
3. 환형 연결 리스트 (Cicurlar Linked List)
- 마지막 노드가 첫 번쨰 노드를 가리키는 연결을 가지는 리스트이다.
- 단일 연결 리스트나 이중 연결 리스트일 수 있다.
* linked list 장점
- 데이터 요소의 삽입과 삭제가 배열에 비해 간단하다. 특정 인덱스에 있는 요소를 삽입하거나 삭제할 때 배열과 달리 요소를 이동시킬 필요가 없다
- 메모리를 효율적으로 사용 가능하다. 데이터가 연속적으로 저장되지 않아도 되므로 메모리의 빈틈 없이 사용할 수 있다.
* linked list 단점
- 임의의 요소에 바로 접근하는 것이 배열에 비해 어려울 수 있다. 특정 인덱스에 직접 접근하기 위해서는 처음부터 순차적으로 탐색해야 한다
- 각 노드가 다음 노드를 가리키는 포인터를 가지고 있기 떄문에 각 노드마다 추가적인 매모리 공간이 필요하다
class Node {
constructor(data) {
this.data = data;
this.next = null;
}
}
class LinkedList {
constructor() {
this.head = null;
}
append(data) {
const newNode = new Node(data);
if(!this.head) {
this.head = newNode;
return;
}
let current = this.head;
while(current.next) {
current = current.next;
}
current.next = newNode;
}
printList() {
let current = this.head;
let listString = '';
while(current) {
listString += `${current.data} -> `;
current = current.next;
}
listString += 'null';
console.log(listString);
}
search(data) {
let current = this.head;
while(current) {
if(current.data === data) {
return true;
}
current = current.next;
}
return false;
}
remove(data) {
//빈 데이터
if(!this.head) {
return;
}
//삭제할 데이터가 헤드인 경우 다음 노드가 헤드
if(this.head.data === data) {
this.head = this.head.next;
return;
}
let current = this.head;
let prev = null;
while(current) {
if(current.data === data) {
prev.next = current.next;
return;
}
//이전 노드의 링크를 다음 노드로 변경하여 현재 노드 삭제
prev = current;
current = current.next;
}
}
}
let linkedList = new LinkedList();
linkedList.append(1);
linkedList.append(2);
linkedList.append(3);
console.log(linkedList);
linkedList.printList(); // 1 -> 2 -> 3 -> null
console.log(linkedList.search(2)); //true
linkedList.remove(1);
linkedList.printList(); // 2 -> 3 -> null
자료 구조 (트리, tree)
* 출처 : https://www.zerocho.com/category/Algorithm/post/580ed6eb77023c0015ee9686
트리(Tree)는 계층적인 데이터를 표현하는 비선형 자료구조입니다. 트리는 노드(Node)들의 집합으로 구성되어 있으며, 부모 (Parent)와 자식(Children) 관계를 가진 노드들의 구조를 나타낸다. 부모 노드는 자식 노드를 가리키며, 각 노드는 0개 이상의 자식을 가질 수 있습니다. 트리 구조에서는 각 노드는 단 하나의 부모 노드를 가진다.(루트 노드 제외)
- 루트 노드(Root Node)
- 트리 구조에서 가장 상위에 있는 노드로, 다른 모든 노드들은 이 루트 노드를 따라 계층적으로 구성된다. 트리는 오직 하나의 루트 노드만을 가진다
- 부모 노드(Parent Node)
- 다른 하나 이상의 노드를 가리키는 노드
- 자식 노드(Children Node)
- 부모 노드에 의해 가리키는 노드로, 부모 노드 바로 아래에 위치한 노드들을 가리킨다
- 리프 노드(Leaf Node)
- 자식 노드가 없는 노드로, 트리의 가장 끝단에 위치한 노드를 의미
- 서브 트리(Subtree)
- 트리 내에서 하나의 노드와 그 노드의 모든 자손 노드로 이루어진 부분 트리를 의미
트리는 다양한 용도로 활용되며, 컴퓨터 과학 및 프로그래밍에서 많은 분야에서 사용된다. 예를 들어 파일 시스템, 데이터베이스, 그래프 알고리즘, 검색 알고리즘 등에서 효과적으로 활용된다.
- 이진 트리(Binary Tree)
- 각 노드가 최대 두개의 자식을 가질 수 있는 트리. 각 노드는 왼쪽 자식과 오른쪽 자식을 가질 수 있다.
- 이진 탐색 트리(Binary Search Tree, BST)
- 이진 트리의 한 종류로, 왼쪽 자식 노드는 해당 부모 노드보다 작고 오른쪽 자식 노드는 해당 부모 노드보다 큰 값을 가지는 조건을 만족한다. 이로 인해 탐색, 삽입 및 삭제 작업이 빠르게 수행된다
- 균형 트리(Balanced Tree)
- 트리의 높이가 최소화되어 있는 트리로, 검색, 삽입, 삭제 연산의 시간 복잡도를 균등하게 유지하는 트리 이다. 대표적으로 AVL 트리, 레드-블랙 트리 등이 있다
트리는 재귀적인 구조를 가지고 있기 때문에, 많은 경우 재귀 알고리즘이 트리와 관련된 작업을 수행하는데 유용하게 사용된다. 이러한 특성들로 인해 트리는 데이터 검색, 정렬, 저장 등의 다양한 문제에 대해 효율적인 해결책을 제공한다.
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
//이진 트리
class BinaryTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new Node(value);
if(!this.root) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
//큰 값이 오른쪽
insertNode(node, newNode) {
if(newNode.value < node.value) {
if(!node.left) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if(!node.right) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}
find(value) {
return this.findNode(this.root, value);
}
findNode(node, value) {
if(!node) {
return null;
}
if(value === node.value) {
return node;
} else if(value < node.value) {
return this.findNode(node.left, value);
} else {
return this.findNode(node.right, value);
}
}
remove(value) {
this.root = this.removeNode(this.root, value);
}
removeNode(node, value) {
if(!node) {
return null;
}
if(value === node.value) {
if(!node.left && !node.right) {
//자식 노드가 없는 경우(단말 노드)
return null;
} else if(!node.left) {
//오른쪽 자식 노드만 있는 경우
return node.right;
} else if(!node.right) {
//왼쪽 자식 노드만 있는 경우
return node.left;
} else {
//양쪽 자식 노드가 모두 있는 경우
let tempNode = this.findMinNode(node.right);//오른쪽 서브 트리에서 가장 작은 값을 찾음
node.value = tempNode.value; //대체할 노드 값 복사
node.right = this.removeNode(node.right, tempNode.value); //대체할 노드를 삭제
return node;
}
} else if(value < node.value) {
node.left = this.removeNode(node.left, value); //왼쪼 서브 트리에서 삭제
return node;
} else {
node.right = this.removeNode(node.right, value); //오른쪽 서브 트리에서 삭제
return node;
}
}
findMinNode(node) {
while(node && node.left !== null) {
node = node.left;
}
return node;
}
// 전위 순회
preorderTraversal(node = this.root) {
if(node) {
console.log(node.value);
this.preorderTraversal(node.left);
this.preorderTraversal(node.right);
}
}
//중위 순회
inorderTraversal(node = this.root) {
if(node) {
this.inorderTraversal(node.left);
console.log(node.value);
this.inorderTraversal(node.right);
}
}
//후위 순회
postorderTraversal(node = this.root) {
if(node) {
this.inorderTraversal(node.left);
this.inorderTraversal(node.right);
console.log(node.value);
}
}
}
const binaryTree = new BinaryTree();
binaryTree.insert(10);
binaryTree.insert(5);
binaryTree.insert(15);
binaryTree.insert(3);
binaryTree.insert(7);
console.log('binaryTree find (7):');
console.log(binaryTree.find(7)); //Node {value: 7, left: null, right: null}
console.log('binaryTree remove (7):');
binaryTree.remove(7);
console.log('binaryTree find (7):');
console.log(binaryTree.find(7)); //Node {value: 7, left: null, right: null}
//전위 순회: 루트 > 왼쪽 > 오른쪽
// 10 5 3 7 15
console.log('Preorder Traversal:');
binaryTree.preorderTraversal();
//중위 순회: 왼쪽 > 루트 > 오른쪽
//3 5 7 10 15
console.log('\nInorder Traversal:');
binaryTree.inorderTraversal();
//후위 순회: 왼쪽 > 오른쪽 > 루트
//3 5 7 15 10
console.log('\nPostorder Traversal:');
binaryTree.postorderTraversal();
자료구조 (힙, Heap), 힙 정렬 Heap sort
출처
https://www.zerocho.com/category/Algorithm/post/582de223d4416a001860e763

힙 정렬 (Heap Sort)는 선택 정렬(Selection Sort)의 한 종류로, 비교 기반의 정렬 알고리즘 중 하나 이다. 주로 배열로 구현되며, 특히 힙 자료구조를 활용하여 정렬하는 방법 이다.
힙(Heap) 이란?
- 힙은 부모 노드의 값이 항상 자식 노드의 값보다 크거나 작은 이진 트리 구조 이다.
- 보통 두 가지 종류의 힙이 있다. 최대 힙(Max Heap)과 최소 힙(Min Heap)
- 최대 힙에서는 부모 노드의 값이 자식 노드의 값보다 크거나 같고, 최소 힙에서는 부모 노드의 값이 자식 노드의 값보다 작거나 같다.
힙 정렬 과정
- 초기 배열을 힙으로 만들기
- 주어진 배열을 최대 힙 혹은 최소 힙으로 구성한다. 이를 위해 배열을 힙으로 변환하는 heapify 과정을 거친다
- 힙에서 최대(최소)값을 추출하여 정렬된 배열에 추가하기
- 최대 힙(또는 최소 힙)에서 루트 노드 값을 추출하고, 추출된 값을 정렬된 배열의 가장 뒤에 추가한다. 그 후 힙의 크기를 줄이고, 다시 heapfiy를 수행하여 힙 속성을 유지한다
- 반복
- 위의 과정을 힙의 크기가 1보다 큰 동안 반복한다. 이렇게 함으로써, 배열에 오름차순(또는 내림차순)으로 정렬된 값들이 저장된다.
힙 정렬의 특징
- 시간 복잡도
- 평균 및 최악의 경우에도 O(n log n)의 시간 복잡도를 가진다
- 제자리 정렬(in-place)
- 힙 정렬은 입력 배열 이외에 추가적은 메모리를 필요로 하지 않는다
- 불안정 정렬(Unstable Sort)
- 동일한 값에 대해서는 정렬 이후에도 상대적인 순서가 유지되지 않을 수 있다.
자료구조 AVL 트리(tree)
출처
https://www.zerocho.com/category/Algorithm/post/583cacb648a7340018ac73f1
(Algorithm) 자료구조(AVL 트리(tree))
안녕하세요. 이번 시간에는 자료구조 끝판왕 AVL 트리에 대해 알아보겠습니다. 가장 복잡하고 가장 어려운 강좌가 될 거 같습니다. 저도 구현하는 데 엄청 애를 먹었던 자료구조입니다. 전전 시
www.zerocho.com
AVL 트리는 이진 탐색 트리(Binary Search Tree, BST)의 일종으로, 균형을 유지하는 자가균형트리(Self-Balncing Tree)의 대표적인 예시 이다. AVL 트리는 데이터를 저장하는 데 사용되며, 탐색, 삽입, 삭제, 연산 등의 작업에서 빠른 성능을 제공한다.
이진 탐색 트리(BST)
BST는 각 노드가 최대 두 개의 자식 노드를 갖는 트리 구조로, 왼쪽 서브트리의 모든 노드는 현재 노드보다 작고, 오른쪽 서브트리의 모든 노드는 현재 노드보다 큰 값으 가지는 특성을 갖는다. 이 특성은 탐색 시간을 평균적으로 O(log n)으로 만들어 준다. 하지만 데이터가 정렬되어 입력될 경우 트리는 한쪽으로 치우쳐질 수 있으며, 이는 탐색 성능이 O(n)으로 떨어지는 최악의 경우를 발생 시킨다.
또한, . AVL 트리는 모든 노드의 왼쪽과 오른쪽 서브트리의 높이 차이가 1 이하를 유지하여 균형을 유지합니다. 여기서 높이 차이가 1보다 크면 균형이 무너진 것으로 간주되며, 이를 회복하기 위해 LL, RR, LR, RL 회전 연산을 사용하여 불균형을 균형있는 트리로 반들어줄 수 있다.
AVL 트리
AVL 트리는 이러한 문제점을 해결하기 위해 제안된 자가균형트리의 일종이다. 이 트리는 아래와 같은 특징을 갖는다.
- 균형 인수(Balance Factor): 각 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이를 나타내는 값으로, -1, 0, 1 세 가지 값 중 하나를 갖는다
- 균형 재조정: 삽입, 삭제 연산을 수행할 때 균형 인수를 유지하기 위해 회전 연산을 사용하여 트리를 재조정한다
- 회전 연산: LL(Left - Left), RR(Right-Right), LR(Left-Right), RL(Right-Left)의 네가지 종류가 있으며, 이를 통해 불균형 상태를 균형있게 만든다
LL(Left-Left) 회전
LL 회전은 새로운 노드가 기존 노드의 왼쪽 서브트리의 왼쪽에 삽입되는 경우 발생합니다. 이로 인해 왼쪽 자식의 왼쪽 서브트리에 노드가 추가되면서 왼쪽 서브트리의 높이가 증가합니다. 이는 균형을 깨뜨리고, 이를 회복하기 위해 우측 회전을 수행합니다.
RR(Right-Right) 회전
RR 회전은 새로운 노드가 기존 노드의 오른쪽 서브트리의 오른쪽에 삽입되는 경우 발생합니다. 이로 인해 오른쪽 자식의 오른쪽 서브트리에 노드가 추가되면서 오른쪽 서브트리의 높이가 증가합니다. 이는 균형을 깨뜨리고, 이를 회복하기 위해 좌측 회전을 수행합니다.
LR(Left-Right) 회전
LR 회전은 새로운 노드가 기존 노드의 왼쪽 서브트리의 오른쪽에 삽입되는 경우 발생합니다. 이로 인해 왼쪽 자식의 오른쪽 서브트리에 노드가 추가되면서 왼쪽 서브트리의 높이 차이가 2 이상이 됩니다. 이를 회복하기 위해 두 단계의 회전이 필요하며, LR 회전은 좌측 회전(LL 회전) 다음에 우측 회전(RR 회전)을 수행하여 균형을 회복합니다.
RL(Right-Left) 회전
RL 회전은 새로운 노드가 기존 노드의 오른쪽 서브트리의 왼쪽에 삽입되는 경우 발생합니다. 이로 인해 오른쪽 자식의 왼쪽 서브트리에 노드가 추가되면서 오른쪽 서브트리의 높이 차이가 2 이상이 됩니다. 이를 회복하기 위해 두 단계의 회전이 필요하며, RL 회전은 우측 회전(RR 회전) 다음에 좌측 회전(LL 회전)을 수행하여 균형을 회복합니다.
AVL 트리 작동 방식
- 노드 삽입: 노드를 BST에 추가한 후, 부모 노드로부터 시작하여 루트 노트까지 거슬러 올라가며 각 노드의 균현 인수를 갱신하고, 필요에 따라 회전 연산을 수행하여 균형을 유지한다.
- 노드 삭제: 삭제된 후에도 트리가 여전히 균형을 유지하도록 회전 연산을 수행하여 균형을 재조정합니다.
시간복잡도
AVL 트리에서의 탐색, 삽입, 삭제 작업은 모두 O(log n)의 시간 복잡도를 갖는다. 하지만 AVL 트리의 균형을 유지하기 위해 추가되는 회전 연산은 이러한 작업을 약간 더 느리게 만들 수 있다.
AVL 트리는 데이터의 동적인 삽입, 삭제가 번번하게 발생하는 상황에서 유용하며, 빠른 검색과 높은 성능을 제공하는 자료구조이다.
//AVL 노드 정의
class AVLNode {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
this.height = 1;
}
}
//AVL 트리 클래스 정의
class AVLTree {
constructor() {
this.root = null;
}
//노드의 높이를 반환
height(node) {
if(node === null) return 0;
return node.height;
}
//노드의 균형 인수를 반환
getBalanceFactor(node) {
if(node === null) return 0;
return this.height(node.left) - this.height(node.right);
}
//좌측 회전
leftRotate(x) {
console.log('\n---- [leftRotate()] ----');
const y = x.right;
const T2 = y.left;
y.left = x;
x.right = T2;
x.height = Math.max(this.height(x.left), this.height(x.right)) + 1;
y.height = Math.max(this.height(y.left), this.height(y.right)) + 1;
return y;
}
//우측 회전
rightRotate(y) {
console.log('\n---- [rightRotate()] ----');
console.log('y: ', y);
const x = y.left;
const T2 = x.right;
x.right = y;
y.left = T2;
y.height = Math.max(this.height(y.left), this.height(y.right)) + 1;
x.height = Math.max(this.height(x.left), this.height(x.right)) + 1;
return x;
}
//삽입 연산
insert(node, key) {
if(node === null) return new AVLNode(key);
if(key < node.key) {
node.left = this.insert(node.left, key);
} else if(key > node.key) {
node.right = this.insert(node.right, key);
} else {
return node; //중복된 키는 허용하지 않음
}
//높이 갱신
node.height = 1 + Math.max(this.height(node.left), this.height(node.right));
//균형 인수 구하기
const balanceFactor = this.getBalanceFactor(node);
console.log('balanceFactor: ', balanceFactor);
//군형을 회복하기 위한 회전 연산 수행
if(balanceFactor > 1 && key < node.left.key) { //LL
console.log('\n---- [Left-Left Rotate] ----');
return this.rightRotate(node);
}
if(balanceFactor < -1 && key > node.right.key) { //RR
console.log('\n---- [Right-Right Rotate] ----');
return this.leftRotate(node);
}
if(balanceFactor > 1 && key > node.left.key) { //RL
node.left = this.leftRotate(node.left);
return this.rightRotate(node);
}
if(balanceFactor < -1 && key < node.right.key) { //LR
node.right = this.rightRotate(node.right);
return this.leftRotate(node);
}
return node;
}
//트리에 노드 추가
insertNode(key) {
this.root = this.insert(this.root, key);
console.log('\n---- [RESULT] ----');
console.log(this.root);
}
//중위 순회로 트리 출력
inOrderTraversal(node) {
if(node !== null) {
this.inOrderTraversal(node.left);
console.log(node.key);
this.inOrderTraversal(node.right);
}
}
//AVL 트리 출력
print() {
this.inOrderTraversal(this.root);
}
}
const avlTree = new AVLTree();
//RR
avlTree.insertNode(10);
avlTree.insertNode(20);
avlTree.insertNode(30);
//LL
// avlTree.insertNode(20);
// avlTree.insertNode(18);
// avlTree.insertNode(12);
//RL
// avlTree.insertNode(12);
// avlTree.insertNode(4);
// avlTree.insertNode(8);
/*
12
4
8
12
8
4
8
4 12
*/
//LR
// avlTree.insertNode(12);
// avlTree.insertNode(15);
// avlTree.insertNode(8);
/*
12
15
8
12
8
15
12
8 15
*/
avlTree.print();
그래프(graph)
참고
https://www.zerocho.com/category/Algorithm/post/584b9033580277001862f16c
(Algorithm) 그래프(graph) - 자료구조
안녕하세요. 이번 시간에는 그래프에 대해 알아보겠습니다. 그래프는 이후에 나올 많은 알고리즘에서 사용되기 때문에 꼭 알아두셔야 합니다. 그래프는 트리와 비슷하게 노드와 엣지로 구성되
www.zerocho.com
Graph
그래프는 노드(또는 버텍스)들이 엣지(또는 아크)로 연결된 추상적인 자료 구조입니다. 실제로 많은 현실 세계의 문제들을 그래프로 모델링하여 해결합니다. 그래프는 노드들 간의 관계를 시각화하고 나타내며, 다양한 문제를 해결하기 위한 중요한 도구로 사용됩니다.
- 트리와 비슷하게 노드와 엣지로 구성되어 있음
- 그래프는 노드: 버텍스, 엣지: 아크
- 버텍스 간에 여러 개의 아크가 존재할 수 도 있다.
- 다른 버텍스에서부터 오는 아크의 개수: In-degree
- 다른 버텍스로 가는 아크의 개수: out-degree
- (방향성을 띄고 있는지에 따라서 방향 그래프(Directed graph) 와 무방향 그래프(Undirected graph)로 나뉜다.
활용
- 네트워크 모델링: 컴퓨터 네트워크, 소셜 네트워크, 교통 네트워크 등을 모델링할 때 사용됩니다.
- 경로 탐색 문제: 최단 경로, 최소 비용 경로 등을 찾는 문제에 활용됩니다.
- 일정 최적화: 리소스 할당, 일정 관리 등에서 최적의 해결책을 찾는 데 활용됩니다.
- 의사 결정 문제: 여러 선택지 간의 최선의 결정을 내리는 데 사용됩니다.
그래프 알고리즘
- 최단 경로 알고리즘: 두 노드 간의 최단 경로를 찾는 알고리즘으로, 다익스트라, 벨만-포드, 플로이드-와샬 등이 있습니다.
- 최소 신장 트리 알고리즘: 그래프 내의 모든 노드를 최소 비용으로 연결하는 트리를 찾는 알고리즘으로, 크루스칼, 프림 등이 있습니다.
- 순회 알고리즘: 그래프 내의 모든 노드를 방문하는 알고리즘으로, 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있습니다.
방향 그래프
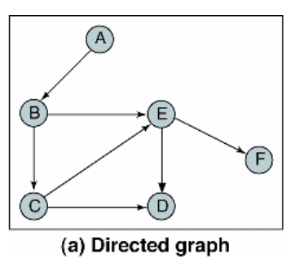
무방향 그래프
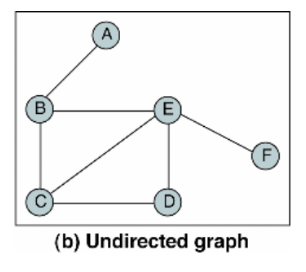
연결 리스트

이차원 배열

(연결 리스트) 무방향 그래프(Undirected graph) BFS 알고리즘 예시
- 너비 우선 탐색(BFS) 알고리즘
: 너비 우선 탐색(BFS, Breadth-First Search)은 그래프 또는 트리에서 시작 정점(노드)으로부터 인접한 노드들을 우선적으로 탐색하는 알고리즘입니다. 이 알고리즘은 시작 정점으로부터 가까운 노드들을 먼저 탐색하고, 그 다음으로는 그 노드들의 이웃 노드들을 순차적으로 탐색합니다.
/*
A - B - D
|
C - E
A: ['B', 'C']
B: ['A', 'D']
C: ['A', 'E']
D: ['B']
E: ['C']
*/
class Graph {
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
console.log('\n --- addVertex ---]');
if(!this.adjacencyList[vertex]) {
this.adjacencyList[vertex] = [];
}
console.log(this.adjacencyList);
}
addEdge(v1, v2) {
console.log('\n --- addEdge ---]');
this.adjacencyList[v1].push(v2);
this.adjacencyList[v2].push(v1);
console.log(this.adjacencyList);
}
bfs(startingVetex) {
const visited = {};
const result = [];
const queue = [startingVetex];
visited[startingVetex] = true;
while(queue.length) {
const currentVertex = queue.shift();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if(!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
});
}
return result;
}
}
const graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('B', 'D');
graph.addEdge('C', 'E');
console.log(graph.bfs('A'));
//['A', 'B', 'C', 'D', 'E']
(이차원 배열) 무방향 그래프(Undirected graph) DFS 알고리즘 예시
- 이차원 배열을 이용한 깊이 우선 탐색(DFS) 알고리즘
: 깊이 우선 탐색(DFS, Depth-First Search)은 그래프나 트리에서 주어진 시작 노드(혹은 루트 노드)에서 시작하여 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 알고리즘입니다. 이 알고리즘은 더 이상 방문할 노드가 없을 때까지 각 분기를 탐색합니다.
DFS는 스택(Stack)이나 재귀 함수를 활용하여 구현됩니다. 각 노드를 방문하고, 그 노드의 이웃 노드들을 모두 탐색하기 전까지는 계속해서 해당 노드의 자식 노드나 이웃 노드를 탐색
class Graph {
constructor(numOfVertices) {
console.log('--- init ---');
this.numOfVertices = numOfVertices;
this.adjacencyMartrix = Array.from({ length: numOfVertices }, () => Array(numOfVertices).fill(0));
console.log('numOfVertices: ', this.numOfVertices);
// 5
console.log('adjacencyMartrix: ', this.adjacencyMartrix);
/*
(5) [0, 0, 0, 0, 0]
(5) [0, 0, 0, 0, 0]
(5) [0, 0, 0, 0, 0]
(5) [0, 0, 0, 0, 0]
(5) [0, 0, 0, 0, 0]
*/
}
addEdge(v1, v2) {
console.log('\n --- addEdge ---');
this.adjacencyMartrix[v1][v2] = 1;
this.adjacencyMartrix[v2][v1] = 1;
console.log('adjacencyMartrix: ', this.adjacencyMartrix);
/*
A B C D E
A [0, 1, 1, 0, 0]
B [1, 0, 0, 1, 0]
C [1, 0, 0, 0, 1]
D [0, 1, 0, 0, 0]
E [0, 0, 1, 0, 0]
C - E
/ |
/ |
A - B
| /
| /
D
*/
}
dfs(startingVertex) {
console.log('\n --- dfs ---');
const visited = Array(this.numOfVertices).fill(false);
console.log('visited: ', visited);
this._dfsHelper(startingVertex, visited);
}
_dfsHelper(vertex, visited) {
console.log('\n --- _dfsHelper ---');
visited[vertex] = true;
console.log(vertex);
for(let i = 0; i < this.numOfVertices; i++) {
if(this.adjacencyMartrix[vertex][i] && !visited[i]) {
this._dfsHelper(i, visited);
}
}
}
}
const graph = new Graph(5);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 4);
console.log('DFS traversal staring from vertex 0:');
graph.dfs(0);
// 0 (A) -> 1 (B) -> 3 (D) -> 2 (C) -> 4 (E)
(연결 리스트) 방향 그래프(Undirected graph) 예시
class Node {
constructor(value) {
this.value = value;
this.edges = [];
}
addEdge(node) {
this.edges.push(node);
}
getEdges() {
return this.edges;
}
}
class Graph {
constructor() {
this.nodes = {};
}
addNode(value) {
this.nodes[value] = new Node(value);
console.log('Graph: ', this.nodes);
/*
nodes = {
1 : { value:1, edgeds: [] }
2 : { value:2, edgeds: [] }
3 : { value:3, edgeds: [] }
4 : { value:4, edgeds: [] }
}
*/
}
addDirectedEdge(source, destination) {
if(!this.nodes[source] || !this.nodes[destination]) {
throw new Error('Node does not exist');
}
this.nodes[source].addEdge(this.nodes[destination]);
console.log(this.nodes);
}
getEdgesOfNode(value) {
if(!this.nodes[value]) {
throw new Error('Node does not exist');
}
return this.nodes[value].getEdges().map(node => node.value);
}
}
const graph = new Graph();
graph.addNode(1);
graph.addNode(2);
graph.addNode(3);
graph.addNode(4);
graph.addDirectedEdge(1, 2);
graph.addDirectedEdge(1, 3);
graph.addDirectedEdge(2, 4);
graph.addDirectedEdge(3, 4);
console.log(graph.getEdgesOfNode(1)); // 출력: [2, 3]
console.log(graph.getEdgesOfNode(2)); // 출력: [4]
console.log(graph.getEdgesOfNode(3)); // 출력: [4]
(이차원 배열) 방향 그래프(Undirected graph) 예시
class Graph {
constructor(numOfVertices) {
this.numOfVertices = numOfVertices;
this.adjacencyMatrix = new Array(numOfVertices).fill(null).map(() => new Array(numOfVertices).fill(0));
}
addEdge(v1, v2) {
if (v1 >= 0 && v1 < this.numOfVertices && v2 >= 0 && v2 < this.numOfVertices) {
this.adjacencyMatrix[v1][v2] = 1; // v1에서 v2로의 간선 추가
} else {
throw new Error('Invalid vertices');
}
}
printGraph() {
for (let i = 0; i < this.numOfVertices; i++) {
let output = `${i} ->`;
for (let j = 0; j < this.numOfVertices; j++) {
if (this.adjacencyMatrix[i][j] === 1) {
output += ` ${j}`;
}
}
console.log(output);
}
}
}
// 예시
const numOfVertices = 5;
const graph = new Graph(numOfVertices);
graph.addEdge(0, 1);
graph.addEdge(0, 4);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 3);
graph.addEdge(3, 4);
graph.printGraph();
// 0 --> 1 --> 2 --> 3 --> 4
// | | ^
// v v |
// 4 <-- 3 <-- 1 <---------
/*
0 -> 1 4
1 -> 2 3 4
2 -> 3
3 -> 4
4 ->
*/
메모이제이션(Memoization)
동적 프로그래밍의 한 기법으로, 이전에 계산한 값을 저장하여 다시 계산하지 않고 필요할 때 재활용하는 것을 의미한다. 이를 통해 프로그램 실행 시간을 줄이고 성능을 향상 시킬 수 있다.
이 기법은 주로 재귀적인 알고리즘에서 중복되는 계산을 피하기 위해 사용된다. 예를 들어, 피보나치 수열과 같이 재귀적으로 정의되는 문제에서는 같은 값을 여러 번 계산하는 경우가 많습니다. 메모이제이션을 사용하면 각 계산 결과를 저장해두고, 동일한 계산이 필요할 때 이전에 계산한 값을 바로 반환하여 중복 계산을 피할 수 있다.
메모이제이션은 일반적으로 배열이나 해시 테이블과 같은 자료구조를 사용하여 값을 저장한다. 이를 위해 함수 내부나 외부에 캐시(cache)를 구현하여 이전에 계산한 결과를 저장하고, 필요할 때마다 캐시에서 값을 가져와 사용합니다.
5의 계승 구하기
let cache = {};
function factorial(n) {
if(n in cache) {
return cache[n];
}
let result;
if(n === 0 || n === 1) {
result = 1;
} else {
result = n * factorial(n - 1);
}
cache[n] = result;
return result;
}
//5의 계승 구하기
// 5 x 4 x 3 x 2 x 1 = 120
console.log(factorial(5));
동적 프로그래밍 Dynamic programming
출처
https://www.zerocho.com/category/Algorithm/post/584b979a580277001862f182
(Algorithm) 동적 프로그래밍(Dynamic programming) - 배낭 문제, LCS 문제, 막대기 문제
안녕하세요. 이번 시간에는 동적 프로그래밍에 대해 알아보겠습니다. 오랜만에 알고리즘으로 돌아왔습니다. 자료구조는 해시 테이블 빼고는 전부 다루었습니다. 해시 테이블은 이따가 다루겠
www.zerocho.com
막대기 자르기
길이가 4인 막대기를 자를 때 얻을 수 있는 최대 가격은 ? 길이를 2인 막대기를 두개로 나누어서 가격을 5 + 5 = 10 으로 만들거나, 길이가 6인 막대는 자르지 않고 그냥 팔았을 때 최대 17의 가격을 얻을 수 있다.
| 길이(i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 가격(pi) | 0 | 1 | 5 | 8 | 9 | 10 | 17 |
- 길이 i 의 막대기를 자를 때 가능한 경우
- 각 경우별로 자른 막대의 가격과 나머지 부분에 대한 최대 가격을 합산
- 이 중에서 가장 큰 값을 선택하여 길이 i의 막대기에 대한 최대 가격을 결정
길이가 4인 막대 잘라서 얻을 수 있는 최대 가격을 구하기위해서,
길이가 4인 막대를 잘를 수 있는 경우의 수를 나열해보았다.
- 4
- 1, 3
- 2, 2
- 3, 1
- 1, 1, 2
- 1, 2, 1
- 2, 1, 1
- 1,1, 1, 1
길이 별 가격 표에 맞춰서 가격을 계산해보자
- 4 = 9
- 1, 3 = 1 + 8 = 9
- 2, 2 = 5 + 5 = 10 (최대가격)
- 3, 1 = 8 + 1 = 9
- 1, 1, 2 = 1 + 1 + 5 = 7
- 1, 2, 1 = 1 + 5 + 1 = 7
- 2, 1, 1 = 5 + 1 + 1 = 7
- 1, 1, 1, 1 = 1 + 1 + 1 + 1 = 4
- 4에서 1 잘랐을 경우, 나머지 3의 최대가격은?
- 4에서 2 잘랐을 경우, 나머지 2의 최대가격은?
- 4에서 3 잘랐을 경우, 나머지 1의 최대가격은?
- 4에서 4 잘랐을 경우, 나머지 0의 최대가격은?
- 0의 최대가격은 0 일 수 밖에 없다
- 1의 최대가격은, 1을 자른다고 했을 때, 한개 밖에 자르지 못하니까, 1의 길이의 가격은 1이다.
- 2의 최대가격은, (0, 1, 5), 최대가격은 5이다.
- 3의 최대가격은 (0, 1, 5, 8), 최대가격은 8이다.
- 4에서 1 잘랐을 경우, 3의 최대가격은? 8
- 1 길이에 가격은 1
- 3의 최대가격은 8
- 총합은 9
- 4에서 2 잘랐을 경우, 2의 최대가격은? 5
- 2 길이에 가격은 5
- 2의 최대가격은 5
- 총합은 10
- 4에서 3 잘랐을 경우, 1의 최대가격은? 1
- 3 길이에 가격은 8
- 1의 최대가격은 1
- 총합은 9
- 4에서 4 잘랐을 경우, 0의 최대가격은? 0
- 4 길이에 가격은 9
- 0의 최대가격은 0
- 총합은 9
결과적으로 (9, 10, 9, 9) 에서의 최대가격은 10이다.
4에서 2개를 자르고, 나머지가 2개일 경우일때가 최대가격이다.
점화식으로 표현하면
길이: n
n의 길이를 자르고 남은 길이: n - i
최대가격 : Rn
Rn = max(Pi + Rn-i)
4의 길이에서 1개를 잘랐을 때, 나머지 3개 -> P1 + R3
4의 길이에서 2개를 잘랐을 때, 나머지 2개 -> P2 + R2
4의 길이에서 3개를 잘랐을 때, 나머지 1개 -> P3 + R1
4의 길이에서 4개를 잘랐을 때, 나머지 0개 -> P4 + R0
= R4 = max(P1 + R3, P2 + R2, P3 + R1, P4 + R0)
* P1 ~ P4 의 길이에 가격은 알고 있다.
* R3 ~ R0 의 최대가격은 알지 못한다.
function cutRod(length, prices) {
let maxArr = new Array(length + 1).fill(0); //[0, 0, 0, 0, 0]
for (let i = 1; i <= length; i++) {
let maxVal = -1;
for (let j = 1; j <= i; j++) {
/*
길이가 1 일떄 , 최대길이: 0
길이가 2일때, 최대길이:? 길이 1에 최대길이 + 길이 2
길이가 3일때, 최대길이:? 길이 1에 최대길이, 길이2최대길이, 길이 3
*/
maxVal = Math.max(maxVal, maxArr[i - j ] + prices[j]);
}
maxArr[i] = maxVal;
}
return maxArr[length];
}
// 예시 막대기 길이와 가격
const rodLength = 4;
const rodPrices = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30];
// 막대기를 자를 때 얻을 수 있는 최대 가격 계산
const maxProfit = cutRod(rodLength, rodPrices);
console.log("막대기를 자를 때 얻을 수 있는 최대 가격:", maxProfit); //10
최장 공통 부분 수열 문제
최장 공통 부분 수열(LCS) 문제는 두 개의 문자열에서 순서대로 겹치는 문자가 최대 몇 개 인지 구하는 문제 입니다.
예를 들어 ABCBDAB와 BDCABA에서 LCS는 BCAB나 BDAB나 BCBA입니다.
앞에서부터 겹치는 것들을 찾아서 문자열을 만들 때 그것이 가장 길다면 LCS가 되는 거죠.
출처: https://www.acmicpc.net/problem/9251
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
[입력]
첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
[출력]
첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.
[예제 입력]
ACAYKP
CAPCAK
[예제 출력]
4
ACAYKP
CAPCAK
START: 0, FIND: 1
[A]CAYKP / C[A]PCAK
START: 1., FIND: 3
A[C]AYKP / CAP[C]AK
START: 3., FIND: 4
AC[A]YKP / CAPC[A]K
START: 4, FIND: X
ACA[Y]KP / CAPC[A]K
--------------------------------------
START: 1, FIND: 0
A[C]AYKP / [C]APCAK
START: 0, FIND: 1
AC[A]YKP / C[A]PCAK
'Algorithm' 카테고리의 다른 글
| [Algorithm] QuickSort (0) | 2023.09.09 |
|---|---|
| [Algorithm] Bubble Sort (0) | 2023.09.07 |

